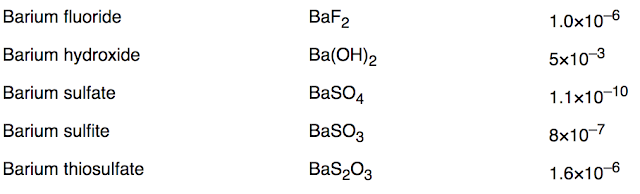Ski Patrol Trail Condition Questions

 

Figure 1: Ski Slope, Full View Uphill

Figure 2: Marking, Skier's Left

Figure 3: Marking, Skier's Right

The ski slope is marked as shown in Figures 1-3. 

1. When assessing the risk of hypothermia in the depicted environment, which factor is most critical? A. Wind chill
   B. Proximity to a heat source
   C. Time of day
   D. Visibility
   E. Wildlife activity

2. Considering avalanche safety, which of the following should be regularly checked in such an environment?
   A. Snowpack stability
   B. Forecasted temperatures
   C. Pathway obstructions
   D. Wildlife migration patterns
   E. Trail markers

3. What is the primary concern for ski patrol when the snow on the trees is as heavy as shown?
   A. Ensuring visibility of trail markers
   B. Monitoring for signs of tree falls
   C. Clearing pathways of snow
   D. Checking for frozen lakes
   E. Patrolling for lost skiers

4. Given the conditions shown, what is the most likely cause of a trail closure?
   A. Ice formation on the path
   B. Low visibility due to fog
   C. Snow overload on branches
   D. Inaccessibility due to heavy snowfall
   E. Daylight limitations

5. Which of these is an essential communication tool for teams in such remote and snowy conditions? A. Mobile phone
   B. Two-way radio
   C. Public address system
   D. Satellite phone
   E. Megaphone

6. When marking hazards on the trail, what characteristic of the markers is most crucial?
   A. Height above the snow
   B. Color contrast with the environment
   C. Frequency along the trail
   D. Reflectiveness
   E. Size of the marker

7. What environmental change should be most closely monitored to prevent hypothermia and frostbite in patrollers?
   A. Snow density
   B. Ambient temperature
   C. Humidity levels
   D. Wind speed
   E. Barometric pressure

8. For patrollers conducting a search operation, what is the most significant terrain challenge indicated by the images?
   A. Steep inclines
   B. Open crevasses
   C. Dense forest areas
   D. Snow-covered paths
   E. Icy patches

9. During end-of-day checks, what is a key environmental sign that patrollers should report?
   A. Decreasing temperatures
   B. Changes in snow texture
   C. Animal tracks
   D. Partially covered trail markers
   E. Melting snow around water bodies

Answers:

1. A
2. A
3. B
4. D
5. B
6. B
7. B
8. C
9. D

Techniques of Partial Fraction Decomposition

Partial fraction decomposition is very often used for many applications, such as integration of rational fractions, inverse Laplace transforms, and Taylor series expansions. In this article, we skip discussions on the basics of partial fraction decomposition in view of many other resources online, however we do highlight techniques to efficiently decompose a fraction into partial fractions.

• Factorization of Polynomials to Linear/Quadratic Factors
• Method of Undetermined Coefficients
• Substitution Method
• Multiplication Method
• Heaviside Cover-up Method
• Partial Fraction Decomposition through Mathematical Software
• Problems

Before we start, we emphasize not to forget the following steps before decomposing the fraction:

1. Ensure the numerator and denominator are both polynomials.
2. Ensure the numerator of the fraction has an order less than the denominator.
3. Ensure the denominator is completely reduced to irreducible factors.

We direct the reader to a document on how to divide polynomials. A table of the decomposition of a fraction of rational functions is provided below.

Irreducible factor in denominator	Term in decomposition
$ax+b$	$\frac{C_1}{ax+b}$
$(ax+b)^n$	$\frac{C_1}{ax+b}+\frac{C_2}{(ax+b)^2}+...+\frac{C_n}{(ax+b)^n}$
$ax^2+bx+c$	$\frac{C_1x+D_1}{ax^2+bx+c}$
$(ax^2+bx+c)^n$	$\frac{C_1x+D_1}{ax^2+bx+c}+\frac{C_2x+D_2}{(ax^2+bx+c)^2}+...+\frac{C_nx+D_n}{(ax^2+bx+c)^n}$

The table above does not include factors of higher order since all higher polynomials must be converted to a multiple of irreducible factors located in the table. This procedure is described below.

Factorization of Polynomials to Linear/Quadratic Factors

Any polynomial can be represented by the product of irreducible, real linear and quadratic factors. This is the result of the fundamental theorem of algebra. The factorization of the rational denominator is required before partial fraction decomposition can commence. There are a few methods to do so, involving the rational root theorem to find linear factors with rational roots. However, this is somewhat restrictive. A more general method for factorizing any polynomial is to first solve (often graphically) for the roots to find the linear factors. After dividing the polynomial by all determined linear factors, the remaining function should be a product of solely irreducible quadratics. The coefficients for the quadratics are found by solving a system of nonlinear equations. This method is best illustrated with a comprehensive example.

Example: Reduce the polynomial into irreducible linear and quadratic factors with real coefficients. $$f(x)=2x^7-9x^6+31x^4-21x^3+24x^2-9x+54$$ At first, this looks extremely intimidating, but initial factorization is simple. Graph the polynomial and it is immediately obvious that two roots exist: $x=-2$ with a multiplicity of 1 and $x=3$ with a multiplicity of 2. Therefore, the linear factors, which are comprised of the real roots, are $x+2$ and $(x-3)^2$ (multiplicity is incorporated as a power). Long division of $f(x)$ with the product of the linear factors produces $g(x)=2x^4-x^3+2x^2+3$. With an order of 4, this function is therefore a product of two quadratics. We denote these two quadratics as: \begin{align*} ax^2+bx+c\\ ux^2+vx+w\end{align*} Multiplying the two polynomials and setting it equal to $g(x)$ results in: $$(au)x^4+(av+bu)x^3+(aw+bv+cu)x^2+(bw+cv)x+cw=2x^4-x^3+2x^2+3$$ Comparison of coefficients yields: \begin{align*} au&=2 \\ av+bu&=-1 \\ aw+bv+cu&=2 \\ bw+cv&=0 \\ cw&=3\end{align*} There are five equations and six unknowns yielding one degree of freedom. We arbitratily set $a=1$ making $u=2$ through the first equation. With some algebra, it can be shown that there are two sets of polynomials that satisfy the equations above. One solution produces the two polynomials $x^2+x+1$ and $2x^2-3x+3$. So, the final answer is: $$f(x)=(x-3)^2(x+2)(x^2+x+1)(2x^2-3x+3)$$ It is significantly easier to do this factorization through a mathematical software. MATLAB provides a function, factor, that can be used for this purpose.

syms x
F = factor(2*x^7-9*x^6+31*x^4-21*x^3+24*x^2-9*x+54)

Output: F = [ x + 2, x^2 + x + 1, 2*x^2 - 3*x + 3, x - 3, x - 3]

Method of Undetermined Coefficients

This method is often used as a fail-safe method for decomposing fractions. The unknown coefficients of the decomposed fractions are solved by forcing the partial fraction decomposition into a form synonymous with the original function. This function will have the same denominator as the original function, with unknown variables all in the numerator. The unknown coefficients are subsequently solved through comparing the two functions' numerators. Consider the function: $$f(x)=\frac{4x^2+6x+6}{x^3-7x-6}$$ By factorizing the denominator through the method described in the previous section, we end up with the following: $$f(x)=\frac{4x^2+6x+6}{(x-3)(x+1)(x+2)}$$ The partial fraction decomposition of the function, let's call $g(x)$, is: $$g(x)=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{x+2}$$ Note that we are solving for the unknown parameters $A,B,C$ to make $f(x)$ and $g(x)$ equal. First, combine the partial fractions into one fraction. This is done by first making the denominators of the individual partial fractions the same as the original function's denominator. $$g(x)=\frac{A}{x-3} \times \frac{(x+1)(x+2)}{(x+1)(x+2)}+\frac{B}{x+1} \times \frac{(x-3)(x+2)}{(x-3)(x+2)}+\frac{C}{x+2} \times \frac{(x-3)(x+1)}{(x-3)(x+1)}$$ We've merely multiplied all the fractions by one, since the multiplying factors all have the same numerator and denominator. $$g(x)=\frac{A(x+1)(x+2)}{(x-3)(x+1)(x+2)}+\frac{B(x-3)(x+2)}{(x-3)(x+1)(x+2)}+\frac{C(x-3)(x+1)}{(x-3)(x+1)(x+2)}$$ $$=\frac{A(x+1)(x+2)+B(x-3)(x+2)+C(x-3)(x+1)}{(x-3)(x+1)(x+2)}$$ At this point, comparing the numerator with the original function's numerator is not useful. We need to force it into the same rational form as the original function's numerator. Thus, we need to simplify the numerator into the form $c_1x^2+c_2x+c_3$. Fortunately this is relatively straightforward but requires some algebra: $$g(x)=\frac{A(x^2+3x+2)+B(x^2-x-6)+C(x^2-2x-3)}{(x-3)(x+1)(x+2)}$$ $$=\frac{Ax^2+3Ax+2A+Bx^2-Bx-6B+Cx^2-2Cx-3C}{(x-3)(x+1)(x+2)}$$ $$=\frac{(A+B+C)x^2+(3A-B-2C)x+(2A-6B-3C)}{(x-3)(x+1)(x+2)}$$ The denominator of both functions $f(x)$ and $g(x)$ are the same, meaning that if the numerators are the same, then the two functions are equal! $$(A+B+C)x^2+(3A-B-2C)x+(2A-6B-3C)=4x^2+6x+6$$ Now that both sides are in the same form, that is, a polynomial of order 2, all that is needed for the numerators to be the same is for the coefficient on the left side to match up with the coefficients on the right hand side. Let us represent this equality slightly differently: \begin{alignat*}{2}(A+B+C)x^2&{}+{}&(3A-B-2C)x&{}+{}&(2A-6B-3C)\\=4x^2&{}+{}&6x&{}+{}&6\end{alignat*} It is now evident that for the coefficients to match up: \begin{alignat*}{2}&A&{}+{}&&B&{}+{}&&C&{}={}&4 \label{eq:1} \tag{1}\\ 3&A&{}-{}&&B&{}-{}&2&C&{}={}&6 \label{eq:2} \tag{2}\\ 2&A&{}-{}&6&B&{}-{}&3&C&{}={}&6 \label{eq:3} \tag{3}\end{alignat*} The first step in solving this system is to subtract equation \ref{eq:2} by equation \ref{eq:3} then by \ref{eq:1} to get $B=-1$. Then multiply equation \ref{eq:1} by 2 and subtract \ref{eq:3} by \ref{eq:1}, yielding $C=2$. Plug in $B$ and $C$ into equation \ref{eq:1} to get $A=3$. Therefore: $$f(x)=\frac{3}{x-3}-\frac{1}{x+1}+\frac{2}{x+2}$$ This method of solving for the unknowns in the partial fraction decomposition works all the time for any sort of partial fraction decomposition. However it is clear that it requires a lot of algebra and thus there is a greater chance calculation errors may arise.

Substitution Method

Consider the previous function again and its partial fraction expansion: $$\frac{4x^2+6x+6}{(x-3)(x+1)(x+2)}=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{x+2}$$ It is important to realize that the equality above must hold for all values of $x$ in the original function's domain. Thus, by simply substituting three arbitrarily different values of $x$ into the equation above, we can derive a system of three equations of $A,B,C$ and solve accordingly. This results in a system of equations that is determined quicker than the previous Method of Undetermined Coefficients. However, a system of equations is still needing to be solved, and for large system of equations, this is very tedious. This method is rarely used to do a complete partial fraction decomposition, however it is used in conjunction with other methods and so the concept is important to understand.

Multiplication Method

This method solves for parameters without necessarily needing to solve systems. Consider the previous function again and its partial fraction expansion: $$\frac{4x^2+6x+6}{(x-3)(x+1)(x+2)}=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{x+2}$$ To solve for $A$, multiply both sides of the equation above by the denominator $x-3$ associated with $A$. Take note that when $x=3, x-3$ is equal to zero. $$\frac{4x^2+6x+6}{(x+1)(x+2)}=A+\frac{B(x-3)}{x+1}+\frac{C(x-3)}{x+2}$$ Now, set $x=3$ as previously found. Parameters $B$ and $C$ are now cancelled with the substitution as they are both multiplied by zero. While using this method, make sure there are no divisions by zero! $$\frac{4(3)^2+6(3)+6}{(3+1)(3+2)}=A+\frac{B(3-3)}{3+1}+\frac{C(3-3)}{3+2}$$ $$\frac{60}{20}=A+0+0$$ $$\therefore A=3$$ Similarly, $B$ and $C$ are found the same way.
Now, let's consider another more complicated partial fraction. Consider the function and its partial fraction expansion: $$\frac{6x^2+9x+3}{(x-1)(x+2)^2}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2} \label{eq:4} \tag{4}$$ $A$ can be found through this method. The steps for showing $A=2$ is omitted. However, note we cannot solve for $B$ using this method. If we proceed to solve for $B$ using this method, we first need to multiply both sides by $x+2$. $$\frac{6x^2+9x+3}{(x-1)(x+2)}=\frac{A(x+2)}{x-1}+B+\frac{C}{x+2}$$ If we substitute $x=-2$, we get a division by zero on the left and right-hand side. However, if we instead solve for $C$, multiplying both sides by $(x+2)^2$ yields: $$\frac{6x^2+9x+3}{x-1}=\frac{A(x+2)^2}{x-1}+B(x+2)+C$$ Substituting $x=-2$ now works: $$\frac{6(-2)^2+9(-2)+3}{-2-1}=\frac{A(-2+2)^2}{-2-1}+B(-2+2)+C$$ $$\therefore C=\frac{9}{-3}=-3$$ To solve for $B$, one may use the Method of Undetermined Coefficients, however it is easier in this case just to use the Substitution method and substitute one number into equation \ref{eq:4}. Any number that does not result in a division by zero can be substituted, so we substitute $x=-1$, which is the root of the numerator in the original function. Note this value is in the domain of the original function. There is no division by zero as a result and the left-hand side of equation \ref{eq:4} goes to zero: $$0=\frac{A}{-1-1}+\frac{B}{-1+2}+\frac{C}{(-1+2)^2}$$ Values of $A$ and $C$ have already been solved using the Multiplication method. $$0=\frac{2}{-1-1}+\frac{B}{-1+2}-\frac{3}{(-1+2)^2}$$ $$\therefore B=1+3=4$$ $$\frac{6x^2+9x+3}{(x-1)(x+2)^2}=\frac{2}{x-1}+\frac{4}{x+2}-\frac{3}{(x+2)^2}$$ Therefore, for the partial fractions that result from repeated linear factors, the Multiplication Method should be used on the associated partial fraction with the denominator raised to the highest power. This method cannot be solely used to solve for the other factors raised to a lower power.
For fractions where the denominator has quadratics or quadratic terms raised to a power, all unknown parameters can be calculated with this method since a division by zero is mitigated. However, the use of complex numbers is required. For example, observe the function and its decomposition below: $$\frac{-x^2 + 3 x - 11}{(x - 2) (x^2 - 2 x + 3)}=\frac{A}{x-2}+\frac{Bx+C}{x^2-2x+3}$$ $A$ is solved easily to yield $A=-3$. To solve for $B$ and $C$, multiply both sides by $x^2-2x+3$. $$\frac{-x^2 + 3 x - 11}{x - 2}=\frac{A(x^2-2x+3)}{x-2}+Bx+C$$ The roots to $x^2-2x+3$ are $1+i\sqrt{2}$ and $1-i\sqrt{2}$. For the first root: $$\frac{-(1+i\sqrt{2})^2+3(1+i\sqrt{2})-11}{1+i\sqrt{2}-2}=\frac{A(0)}{x-2}+B(1+i\sqrt{2})+C$$ $$\frac{-7+i\sqrt{2}}{-1+i\sqrt{2}}=B(1+i\sqrt{2})+C$$ $$3 + 2 i \sqrt{2}=B(1+i\sqrt{2})+C \label{eq:5} \tag{5}$$ At this point, we know $B$ and $C$ must be real numbers, so that automatically forces $B$ to equal 2. Then it follows that $C=1$. A review of complex number operations is located here.
Complex number algebra may be a bit tedious so in this case, the Method of Undetermined Coefficients to solve for $B$ and $C$ may have produced a quicker answer. However, if a fraction has many linear factors in its denominator and only one or two quadratic terms, this method for partial fraction decomposition may be faster compared to the Method of Undetermined Coefficients since this method does not require the tedious step of combining all partial fractions into one fraction.
With the same analysis, it can be shown that for partial fractions that result from repeated quadratic factors, the Multiplication Method should be used on the associated partial fraction with the denominator raised to the highest power. This method cannot be solely used to solve for the other factors raised to a lower power. This is the same conclusion as the case for repeated linear factors.

Heaviside Cover-up Method

The Heaviside Cover-up Method uses the exact method as the Multiplication Method, but removes the intermediate algebra steps to drastically improve the time in solving for the unknown coefficients. It is especially useful for a partial fraction decomposition of many terms. However, it is important that the Heaviside Method has the same requirements presented in the multiplication method; this method works all the time for a decomposition with only linear factors but special exceptions apply for decompositions with other types of factors. Using the same example as before, $$\frac{4x^2+6x+6}{(x-3)(x+1)(x+2)}=\frac{A}{x-3}+\frac{B}{x+1}+\frac{C}{x+2}$$ The decomposition only involved linear factors, and so the Heaviside Cover-up method will work to solve for all parameters. Now, to solve for $A$, first notice that the denominator associated with $A$ in the partial fraction equals zero when $x=3$. Next, we simply 'cover up' or remove the factor $x-3$ associated with $A$ in the original function. $$\frac{4x^2+6x+6}{\hphantom{(x-3)}(x+1)(x+2)}$$ Lastly, we plug in the $x$ value of 3 that we previously solved for and plug it into the remaining function. $$A=\frac{4(3)^2+6(3)+6}{\hphantom{(x-3)}(3+1)(3+2)}=3$$ Solving for $B$ this time, $x=-1$ to solve for the root of the denominator $x+1$ associated with $B$. Next, 'cover up' $x+1$ from the original function. $$\frac{4x^2+6x+6}{(x-3)\hphantom{(x+1)}(x+2)}$$ Substitute $x=-1$ into the remaining function. $$B=\frac{4(-1)^2+6(-1)+6}{(-1-3)\hphantom{(x+1)}(-1+2)}=-1$$ Solve $C$ through the same way. $$C=\frac{4(-2)^2+6(-2)+6}{(-2-3)(-2+1)\hphantom{(x+2)}}=2$$ Now, for the case of non-linear factors in the denominator: $$\frac{4x^2-x-2}{x^2(x-1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x-1}$$ Heaviside method can be used for the fractions with linear denominators as was the case in the multiplication method. $$C=\frac{4(1)^2-1-2}{(1)^2\hphantom{(x-1)}}=1$$ The Heaviside method can be used for the partial fraction with the highest order denominator that resulted from the $x^2$ term: $$B=\frac{4(0)^2-0-2}{\hphantom{x^2}(0-1)}=2$$ The substitution method / method of undetermined coefficients is used to solve for the last unknown parameter. Selecting an arbitrary value to substitute $x=2$, $$\frac{4(2)^2-2-2}{2^2(2-1)}=\frac{A}{2}+\frac{B}{2^2}+\frac{C}{2-1}$$ $$3=\frac{A}{2}+\frac{2}{2^2}+\frac{1}{1}$$ which quickly shows that $A=3$. A table is conveniently provided below to list out restrictions when using the Heaviside method.

Irreducible factor in denominator	Heaviside method restriction
$ax+b$	None.
$(ax+b)^n$	May only be used on associated partial fraction with denominator raised to highest power.
$ax^2+bx+c$	None, complex numbers required. May be quicker to use Method of Undetermined Coefficients.
$(ax^2+bx+c)^n$	May only be used on associated partial fraction with denominator raised to highest power. Complex numbers required. May be quicker to use Method of Undetermined Coefficients.

Partial Fraction Decomposition through Mathematical Software

Given the opportunity, this method is the easiest. MATLAB provides a function, partfrac, that can be used. The function accepts the function, and optionally the independent variable. For the same function given first in the Methods of Undetermined Coefficient method $\frac{4x^2+6x+6}{x^3-7x-6}$, the partial fraction is calculated through the code:

syms x
f=partfrac((4*x^2+6*x+6)/(x^3-7*x-6))

Output: f = 2/(x + 2) - 1/(x + 1) + 3/(x - 3)
Use the optional second parameter to specify the independent variable. In the case of $\frac{a}{(x+a)(x+2)}$, $x$ is the independent variable and $a$ is a constant:

syms x a
f=partfrac(a/((x+a)*(x+2)),x)

Output: f = a/((a - 2)*(x + 2)) - a/((a + x)*(a - 2))

Problems

1. Decompose $f(x)=\frac{4x^2+6x+8}{x^2(x+4)}$ into partial fractions using all the methods shown.
2. Decompose $f(x)=\frac{a}{(x-b)(x-c)}$ into partial fractions, where $a,b,c$ are real numbers and $b \neq c$.

Is BaSO4 soluble or insoluble?

Answer: BaSO4 would typically be considered insoluble due to the presence of a sulfate ion. This usually precludes an ion from disassociating easily in an aqueous solution; this being water. 

The idea of BaSO4 being considered insoluble is further borne out in the Ksp values. While these cannot be directly related to molar solubility, they provide a strong hint that Barium sulfate is more stringent than other comparable molecules. For example Ba(OH)2's ksp is approximately seven orders of magnitude less which means that it is much more likely to ionize. You can tell that the molar solubility of barium hydroxide is orders of magnitude greater without performing the necessary calculations. As a reminder a compound is considered insoluble if less than 1% of the compound ionizes. 

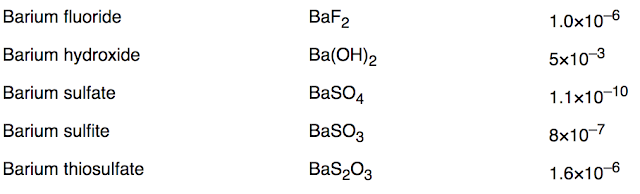ksp values of some common Barium products (source)

What is the molar solubility of BaSO4?

The calculation is based on the chemical equation for the disassociation of BaSO4 and the formula for ksp (equilibrium constants only include aqueous and gaseous species). 

BaSO₄(s) ⇌ Ba²⁺(aq) + SO₄²⁻(aq)

K_sp = [Ba²⁺][SO₄²⁻]

Since when we ionize we create the two ions in equal molar quantity we can state the following

[Ba²⁺] = [SO₄²⁻] = x

$1.1*10^-10 = x^2$

x = $1.05*10^-5$ M

This concentration indicates that less than 1% of the solution is composed of ionized species. 

How does BaSO4 theoretically ionize? 

As the equation (BaSO4 (s) => Ba(2+)(aq) + SO4(2-)(aq)) indicates, barium sulfate would disassociate and produce the barium and sulfate ion. In the real world; however, the low molar solubility indicates that very little barium sulfate actually ionizes. 

What experimental techniques can be utilized in order to verify the solubility of BaSO4?

Experimental observations play a crucial role in confirming the insolubility of barium sulfate. Several methods and techniques are employed to assess the solubility of a compound, and in the case of barium sulfate, the following experimental observations contribute to our understanding of its insolubility:

1. Precipitation Reaction: One common method to demonstrate the limited solubility of barium sulfate is through a precipitation reaction. When a soluble barium salt (e.g., barium chloride, BaCl₂) is added to a solution containing a soluble sulfate salt (e.g., sodium sulfate, Na₂SO₄), a white precipitate of barium sulfate forms. The appearance of the precipitate indicates that the compound is not fully dissolving in the solution, supporting its insoluble nature.

BaCl₂(aq) + Na₂SO₄(aq) → BaSO₄(s) + 2NaCl(aq)

2. Gravimetric Analysis: Gravimetric analysis is a quantitative method used to determine the concentration of a particular species in a solution by measuring its mass. In the case of barium sulfate, after precipitating the compound as mentioned above, the collected precipitate is filtered, washed, and dried to remove any remaining soluble impurities. The mass of the resulting dried barium sulfate is then measured, and from the stoichiometry of the reaction, the concentration of dissolved barium ions can be calculated. The extremely small mass of barium sulfate obtained in these experiments is indicative of its low solubility.

3. Solubility Curves: A solubility curve represents the relationship between temperature and the solubility of a compound. For barium sulfate, a solubility curve can be constructed by determining the concentration of dissolved barium ions at various temperatures. The resulting curve shows that the solubility of barium sulfate is virtually constant over a wide temperature range, consistent with its insoluble nature.

4. Saturation Point: By adding barium sulfate to water and continuously stirring the mixture, a saturation point is eventually reached where no more solid will dissolve, and any additional barium sulfate added will not disappear into the solution. This point is critical as it shows the maximum concentration of dissolved barium ions that can be achieved, providing further evidence of the compound's limited solubility.

Together, these experimental observations provide strong evidence for the insolubility of barium sulfate in water and support the theoretical understanding derived from the thermodynamics and solubility product constant (K_sp) considerations. The combination of theoretical principles and experimental data reinforces our confidence in the knowledge that barium sulfate is indeed highly insoluble in aqueous solutions.

What are the other properties of BaSO4?

Barium sulfate (BaSO₄) possesses several noteworthy properties, some of which are outlined below:

1. Physical State: Barium sulfate is a white, crystalline solid at room temperature. It occurs naturally as the mineral "barite" and is commonly synthesized for various applications.

2. Density: Barium sulfate has a relatively high density, typically around 4.5 grams per cubic centimeter (g/cm³). This density makes it useful for certain applications, such as in radiology as a contrast agent.

3. Insolubility: As previously discussed, barium sulfate is highly insoluble in water and most common solvents. This property contributes to its use in medical imaging procedures (e.g., barium sulfate suspensions for X-ray examinations of the gastrointestinal tract) and as a filler in various materials.

4. Chemical Inertness: Barium sulfate is chemically inert, meaning it does not readily react with other substances under normal conditions. This inertness is advantageous in applications where chemical stability is essential, such as in paints, coatings, and plastics.

5. Non-Toxicity: Barium sulfate is considered non-toxic, which further supports its use in medical applications. When consumed in small quantities (e.g., in medical tests), it passes through the body without being absorbed or causing harm.

6. Refractive Index: Barium sulfate has a relatively high refractive index, making it useful as a filler in products like paint and plastics to enhance opacity and brightness.

7. Thermal Stability: Barium sulfate exhibits good thermal stability, retaining its physical and chemical properties at elevated temperatures. This characteristic makes it suitable for applications in industries where high temperatures are involved.

8. Electrical Insulator: Due to its non-conductive nature, barium sulfate serves as an excellent electrical insulator. This property is valuable in applications where electrical isolation is necessary, such as in electronic devices and insulating materials.

9. X-ray Absorption: Barium sulfate has high X-ray absorption properties, which is why it is used as a contrast agent in medical imaging procedures like barium X-rays. It allows for clear visualization of the gastrointestinal tract and certain anatomical structures.

10. Photographic Uses: Barium sulfate was historically used in black-and-white photography as a white pigment in photographic paper and certain emulsions.

Overall, the unique combination of properties exhibited by barium sulfate makes it valuable in various industrial, medical, and commercial applications. Its insolubility, chemical inertness, and X-ray absorption properties, in particular, make it a versatile and sought-after material in different fields.

Is H2S Polar or Nonpolar?

Answer: H2S is a polar molecule due to the presence of lone pair electrons at the top of the molecule causing a region of partial negative charge due to electron-electron repulsion. 

H2S has a very similar structure as H2O (see the lewis dot structure for H2O and the polar/nonpolar explanation at the linked addresses). However, due to the larger size of the sulfur atom compared to oxygen, the bond angle (i.e. the smaller angle between the two hydrogen atoms) is only 92˚ compared to 107.5˚ for H2O. Sulfur contains many more electrons which ultimately due to electron-electron repulsion require a lot more space. Nevertheless the decreased electronegativity of sulfur when compared to hydrogen (2.58 vs. 2.20, respectively) means that the molecule is much less polar overall when compared to H2O. This means that it has a much lower melting and boiling point at -82˚C and -60˚C, respectively. Like SO2 the presence of sulfur means that this molecule has a pungent odor in gaseous form although it is colorless. 

H2S Ball and Stick Diagram. Created with MolView.

How is H2S utilized in the real world?

Hydrogen sulfide appears in many different ways within the natural world. For starters it is an important constituent of the sulfur cycle. Bacteria oftentimes convert the sulfur from organic elements to inorganic molecules such as H2S. The main use of hydrogen sulfide is as a storage compound which can be converted to pure sulfur during reactions to form all kinds of sulfur-containing compounds. Hydrogen sulfide may have also caused a mass extinction due to its buildup within the atmosphere. Based on this fact it is not difficult to imagine the toxicity of hydrogen sulfide towards life forms such as human beings. It negatively impacts proper nervous system functioning primarily although it will affect other body systems as well. Nevertheless there are certain organisms adapted to live in high-H2S conditions due to those environments existing in deep underwater volcanic sea vents.